在我们谈论渲染之前，我们需要考虑我们要渲染什么，以及我们正在看什么。如果你没有什么可看的，那就没有什么可以渲染的。

现实世界是由形状、外观和结构多种多样的物体组成的。例如，烟雾、椅子和构成海洋的水有什么区别？在计算机图形学中，我们通常喜欢将对象视为固体或非固体。然而，在现实世界中，两者的唯一区别是构成这些物体的物质的密度。烟雾是由松散连接的分子组成，并被大量的空白空间隔开，而制成椅子的木头是由紧密堆积在尽可能小的空间中的分子组成的。但在 CG 中，我们通常只需要定义对象的外部形状（我们将在本课稍后讨论如何渲染非固体对象）。我们该怎么做呢？

在上一课中，我从计算机图形编程简介开始，我们已经介绍了在计算机内存中定义形状的方法，我们需要开始定义 3D 空间中的点的概念。一般来说，一个点被定义为计算机内存中的三个浮点数，代表笛卡尔坐标系的三个轴：x轴、y轴和z轴。从这里，我们可以简单地定义空间中的几个点并将它们连接起来以定义一个表面（多边形）。请注意，多边形应始终共面，这意味着构成面或多边形的所有点应位于同一平面上。通过三个点，您可以创建最简单的形状：三角形。您会看到三角形随处可见，尤其是在光线追踪中，因为已经开发了许多不同的技术来有效计算直线与三角形的交点。当面或多边形具有三个以上的点（也称为顶点）时，将这些面转换为三角形的情况并不少见，这一过程称为三角剖分。

图 1：所有 3D 对象的基本砖块都是三角形。可以通过将 3 个点或顶点（在 2D 或 3D 中）相互连接来创建三角形。通过组装三角形可以创建更复杂的形状。

我们将在本课后面解释为什么将几何图形转换为三角形是一个好主意。但这里的要点是，您可以创建的最简单的表面或对象是三角形，虽然三角形本身并不是很有用，但您可以通过组装三角形来创建更复杂的形状。从很多方面来说，这就是建模的意义所在。该过程与将砖块放在一起以创建更复杂的形状和表面非常相似。

图 2：为了近似曲面，我们沿着曲线的路径对曲线进行采样并将这些样本连接起来。

图 3：您可以使用更多的三角形来改善曲面的曲率，但几何体的渲染会变得更重。

世界不是多边形的！

大多数刚接触计算机图形学的人经常会问，当三角形是平坦且有角度的表面时，如何从三角形创建曲面。首先，我们在 CG 中定义物体表面的方式（使用三角形或多边形）是对现实的非常粗略的表示。在我们看来，看似平坦的表面（例如墙壁的表面），在微观层面上通常是极其复杂的景观。有趣的是，物体的微观结构对其外观有很大影响，而不是对其整体形状有很大影响。但回到主要问题，使用三角形或多边形确实不是表示曲面的最佳方式。它为物体提供了多面外观，有点像切割钻石（这种多面外观可以通过称为平滑着色的技术稍微改善，但平滑着色只是我们在学习着色课程时会学到的技巧） 。如果绘制一条平滑曲线，则可以通过沿该曲线放置几个点并用直线（我们称为线段）连接这些点来近似该曲线。要改进这种近似，您可以简单地减小线段的大小，这与沿曲线创建更多点相同。沿着平滑表面实际放置点或顶点的过程称为采样（将平滑表面转换为三角形网格的过程称为曲面细分。我们将在本章中进一步解释如何定义平滑表面）。同样，对于 3D 形状，我们可以创建更多、更小的三角形，以更好地近似曲面。当然，我们创建的几何体（或三角形）越多，渲染该对象所需的时间就越长。这就是为什么渲染艺术通常需要在用于近似对象曲率的几何体数量与渲染此 3D 模型所需的时间之间找到权衡。您在 3D 模型中放入的几何细节量还取决于您在图像中看到该模型的距离。您离物体越近，您可能想看到的细节就越多。处理模型复杂性也是计算机图形学中一个非常大的研究领域。

图 4：贝塞尔曲线图块及其控制点，在此图像中由橙色网表示。请注意生成的曲面如何不穿过控制点或顶点（曲面边缘除外，这实际上是贝塞尔曲面片的属性）。

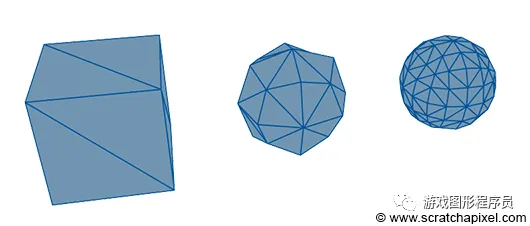
图 5：使用细分曲面算法将立方体变成球体（几乎是球体）。该算法背后的想法是通过递归细分来创建原始网格的更平滑版本。

多边形网格很简单，这就是它们很受欢迎的原因（您在 CG 故事片或游戏中看到的大多数对象都是这样定义的：作为多边形或三角形的集合）但是，正如之前所建议的，它们不适合建模弯曲或有机表面 。当计算机开始用于设计汽车等制造对象 (CAD) 时，这成为一个特殊问题。NURBS 或细分曲面旨在解决这一特定缺点。它们基于这样的想法：点仅定义控制网格，可以通过数学方法计算出完美的曲面。表面本身纯粹是方程的结果，因此不能直接渲染（控制网格也不是，仅用作算法的输入）。它需要被采样，类似于我们之前对曲线进行采样的方式（形成基础或输入网格的点通常称为控制点。这些技术的特点之一是生成的曲面通常不会通过这些控制点）。这种方法的主要优点是您需要更少的点（与获得具有多边形的光滑表面所需的点数量相比更少）来控制完美光滑表面的形状。虽然可以使用多边形创建曲面，但与仅用几个点（如 NURBS 和细分曲面）定义类似形状相比，编辑它们要耗时得多（而且精度仍然较低）。如果它们是优越的，为什么它们没有被到处使用呢？它们比多边形网格的渲染消耗（稍微）更大，因为需要首先从控制网格生成多边形网格（这需要额外的步骤），这就是为什么它们并不总是在游戏中使用（但许多游戏引擎，例如 因为cry引擎实现了它们）。NURBS 总体上比多边形网格更难操作。这就是为什么艺术家通常使用细分曲面，但它们仍然用于需要高精度的设计和 CAD 中。Nurb 和细分曲面将在几何部分中进行研究，但是，在本节的进一步课程中，我们将学习贝塞尔曲线和曲面（用于渲染犹他茶壶），它们在某种程度上与 NURBS 非常相似。

图 6：为了表示烟雾或液体等流体，我们需要在 3D 网格单元中存储体积密度等信息。

在大多数情况下，3D 模型是手工生成的。所谓手工，是指有人在 3D 空间中创建顶点并将它们连接起来以构成对象的面。然而，也可以使用模拟软件来生成几何形状。这通常是产生水、烟或火的方式。特殊程序模拟流体移动的方式并根据该模拟生成多边形网格。在烟雾或火灾的情况下，程序不会生成表面，而是生成 3D 维度网格（划分为等距单元（也称为体素）的矩形或盒子）。该网格的每个单元都可以被视为一小块空间，该空间要么是空的，要么被烟雾占据。烟雾主要由其密度来定义，这是我们将存储在细胞中的信息。密度只是一个浮点数，但由于我们处理的是 3D 网格，所以 512x512x512 网格已经消耗了大约 512Mb 的内存（并且我们可能需要存储比密度更多的数据，例如烟雾或火灾温度、其颜色等） 。每次我们将网格分辨率加倍时，该网格的大小就会增大 8 倍（1024x1024x1024 需要 4Gb 的存储空间）。流体模拟是计算密集型的，模拟生成非常大的文件，渲染体积本身通常比渲染固体对象花费更多的时间（我们需要使用一种称为光线行进的特殊算法，我们将在下一章中简要介绍）。在上图中（图 6），您可以看到在 Maya 中创建的 3D 网格的屏幕截图。

使用光线追踪时，并不总是需要将对象转换为多边形来渲染它。光线追踪需要计算光线（只是直线）与构成场景的几何体的交集。有时可以通过数学方法来确定直线（射线）是否与几何形状相交。

射线与物体相交测试存在代数解。当物体的形状可以通过方程以数学方式定义时，这通常是可能的。更一般地说，您可以将此方程视为表示表面（例如球体表面）整体空间的函数。这些曲面称为隐式曲面（或代数曲面），因为它们是由函数隐式定义的。原理很简单。想象你有两个方程：

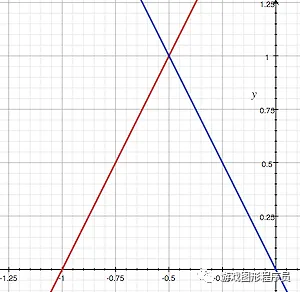
您可以在相邻图像中看到这两个方程的图。这是线性方程组的一个例子。如果您想查明这些方程定义的两条直线是否交于一点，那么它们必须有一个 x，且两个方程给出相同的 y。你可以写成：

求解 x，您将得到：

因为射线也可以用方程来定义，所以这两个方程，即射线方程和定义物体形状的方程，可以像任何其他线性方程组一样求解。如果该线性方程组存在解，则射线与物体相交。

可以使用几何和代数方法找到与射线相交的形状的一个非常好的且简单的示例是球体。您可以在“渲染简单形状”课程中找到对这两种方法的解释。

图 7：元球对于模拟有机形状很有用。

图 8：构造几何的示例。球体定义的体积已从立方体中移除。您可以在左侧看到两个原始对象，在右侧看到最终的形状。

隐式曲面在建模中非常有用，但并不常见（而且肯定不如以前那么常见）。可以使用隐式曲面来创建更复杂的形状（通过布尔运算组合球体、立方体、圆锥体等隐式图元），这种技术称为构造实体几何（或 CSG）。元球（由 Jim Blinn 在 20 世纪 80 年代初发明）是另一种用于创建有机形状的隐式几何形式。

隐式表面的问题是它们不容易渲染。虽然通常可以直接对它们进行光线追踪（我们可以使用代数方法计算光线与隐式曲面的交集，如前所述），但首先需要将它们转换为网格。将隐式曲面转换为网格的过程并不像 NURBS 或细分曲面那么简单，并且需要特殊的算法，例如移动立方体算法（由 Lorensen 和 Cline 于 1987 年提出）。它还可能导致创建重型网格。

查看几何部分，详细了解这些不同的主题。

三角形作为渲染基元

在本系列课程中，我们将通过光线球体相交测试研究隐式曲面的示例。我们还将看到参数化曲面的示例，其中犹他茶壶使用贝塞尔曲面。然而，一般来说，大多数渲染 API 都会选择将不同几何类型实际转换为三角形网格的解决方案，然后渲染三角形网格。这有几个优点。支持多种几何类型，例如多边形网格、隐式或参数化表面，需要为每种支持的表面类型编写射线对象例程。这不仅需要编写更多代码（可能具有明显的缺点），而且如果您做出这种选择，让这些例程在通用框架中工作也很困难，这通常会导致渲染引擎的性能下降 。

请记住，渲染不仅仅是渲染 3D 对象。它还需要支持许多功能，例如运动模糊、位移等。必须支持许多不同的几何表面，意味着这些表面中的每一个都需要与整组支持的功能配合使用，这比所有表面都困难得多 转换为相同的渲染基元，并且如果我们使所有功能仅适用于该单一基元。

如果将代码限制为仅渲染一个图元，通常也会获得更好的性能，因为您可以集中所有精力来非常有效地渲染这一单个图元。三角形通常是光线追踪的首选。为了寻找最佳的（最快/最少的指令、最少的内存使用和最稳定）算法来计算射线与三角形的交集，人们已经进行了大量的研究。然而，其他渲染API（例如OpenGL）也渲染三角形，即使它们不使用光线追踪算法。一般而言，现代 GPU 被设计和优化为基于三角形执行单一类型的渲染。有人（幽默地）就这个话题写道：

因为当前的 GPU 被设计为处理三角形，人们使用三角形，所以 GPU 只需要处理三角形，因此它们被设计为仅处理三角形。

将自己限制为仅渲染一个基元，允许您将常见操作直接构建到硬件中（您可以构建一个非常擅长执行这些操作的组件）。一般来说，三角形很适合使用，原因有很多（包括我们已经提到的）。它们总是共面的，很容易分成更小的三角形，但它们是不可分割的。在三角形上插入纹理坐标的数学也很简单（稍后我们将使用它来将纹理应用到几何体）。这并不意味着 GPU 无法设计为有效渲染任何其他类型的图元（例如四边形）。

3D 场景不仅仅是几何图形

通常，3D 场景不仅仅是几何图形。虽然几何图形是场景中最重要的元素，但您还需要摄像机来观察场景本身。因此，场景描述通常还包括摄像机。没有灯光的场景是黑色的，因此场景也需要灯光。在渲染过程中，所有这些信息（几何体、相机和灯光的描述）都包含在称为场景文件的文件中。3D 场景的内容也可以加载到 3D 软件包（例如 Maya 或 Blender）的内存中。在这种情况下，当用户单击渲染按钮时，特殊程序或插件将遍历场景中包含的每个对象、每个灯光，并将整个对象（包括相机）直接导出到渲染器。最后，您还需要向渲染器提供一些额外的信息，例如最终图像的分辨率等。这些通常称为全局渲染设置或选项。

概括

从本章中您应该记住的是，我们首先需要考虑场景是由什么组成的，然后再考虑下一步，即创建该 3D 场景的图像。场景需要包含三样东西：几何体（要查看的一个或多个 3D 对象）、灯光（没有灯光，场景将是黑色的）和摄像机，用于定义渲染场景的视点。虽然可以使用许多不同的技术来描述几何体（多边形网格、NURBS、细分曲面、隐式曲面等），并且虽然这些类型中的每一种都可以使用适当的算法直接渲染，但仅支持 一种渲染基元。在光线追踪和现代 GPU 中，首选的渲染基元是三角形。因此，通常，在场景渲染之前，几何体将被转换为三角形网格。